Bài toán 7 cây cầu của Ơ-le (Euler)

Làm thế nào để đi qua cả 7 cây cầu mà không lặp lại 1 cái nào?

Không chỉ dừng lại là 1 câu đố, đây là bài toán kinh điển mở ra rất nhiều ứng dụng trong cuộc sống như: Lý thuyết đồ thị và cả topo học.

Lý thuyết đồ thị và topo học là các ngành toán học vô cùng quan trọng, có ứng dụng thực tiễn cao. Tuy nhiên những ngành toán học này lại ra đời khá muộn và xuất phát từ một câu chuyện thực tế vô cùng thú vị.

Hiện tại 7 cây cầu này đã không còn như xưa nhưng Ơ-le đã đưa chúng đi vào lịch sử :) Theo quan sát từ Google map thì hiện chỉ còn 3 cây cầu trong số đó. 4 cây cầu khác được bỏ đi và thay bằng một đường cao tốc trên cao

Câu chuyện 7 cây cầu ở Königsberg

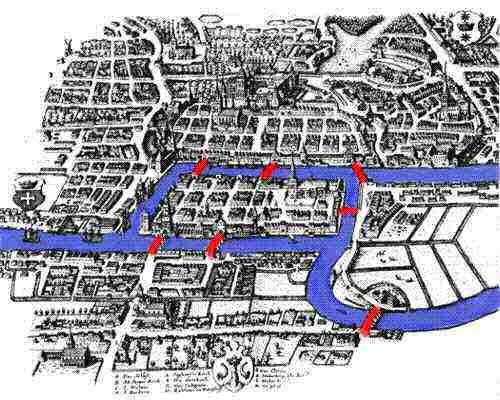
Königsberg là một thành phố nay thuộc nước Nga, ở nơi này có 7 cây cầu. Mỗi cây cầu sẽ nối liền 2 bờ sông, hoặc là một bờ sông với một trong hai cù lao, hoặc nối 2 cù lao với nhau như hình bên dưới:

7 cây cầu (màu đỏ) ở thành phố Königsberg. Ảnh Internet.

Mô hình đơn giản của bài toán. Ảnh Internet.

Người dân ở Königsberg đã đặt ra một câu đố mà chưa từng có ai giải được: "Liệu có thể đi một lần qua tất cả 7 chiếc cầu mà không phải lặp lại hay không (hay mỗi cây cầu chỉ được đi qua một lần duy nhất)?".

Câu đố thú vị khiến nhiều người tới nơi đây và... đi dạo thử để thử sức! Thế nhưng kết quả là họ đều thất bại trong việc tìm một phương án thỏa mãn yêu cầu đưa ra.

Chỉ tới năm 1735, một nhà toán học lỗi lạc tình cờ nghe được câu chuyện này khi tới nơi đây. Người đó chính là thiên tài người Thụy Sĩ Leonhard Euler (1707 - 1783), ông cùng với Newton và Archimedes được xem là 3 nhà toán học vĩ đại nhất thế giới.

Chính ông đã chứng minh được bài toán này không có lời giải hay không thể thực hiện được và việc làm của nhiều người là vô ích khi đâm đầu tìm kiếm một phương án khả thi.

Euler đã giải bài toán này như thế nào?

Thiên tài người Thụy sĩ Leonhard Euler (1707 - 1783). Ảnh Internet.

Thoạt nhìn đây có vẻ là một câu đố bình thường, thế nhưng nó lại ẩn chứa mối liên hệ sâu sắc giữa lý thuyết đồ thị và topo học sau này, chính việc giải bài toán đã giúp Euler mở ra một nhánh mới trong toán học: Lý thuyết đồ thị!

Lời giải của Euler. Ảnh Internet.

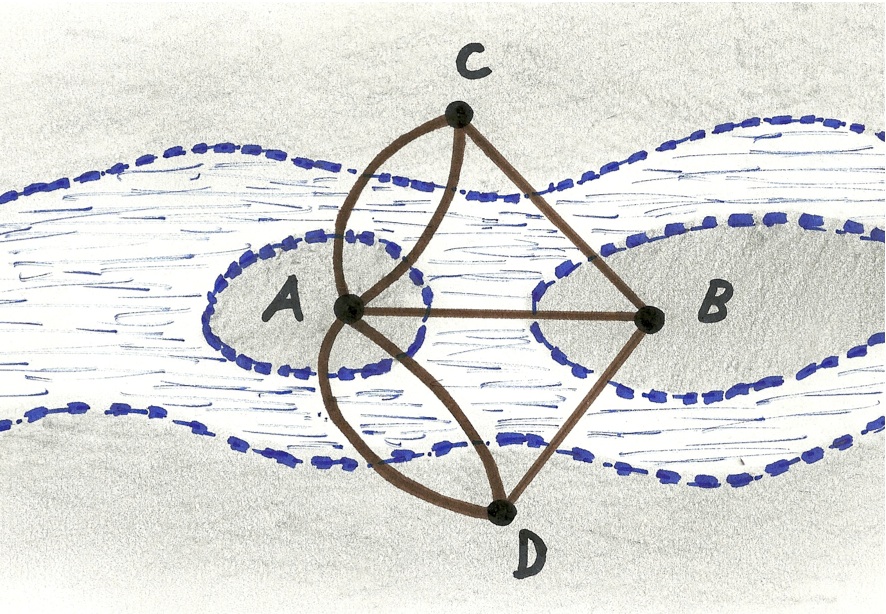
Đầu tiên, Euler tìm cách "mô hình hóa" bài toán một cách trừu tượng nhất thông qua việc biểu diễn các cù lao hay bờ sông bằng các chấm tròn, còn các cây cầu là đoạn thẳng (có thể là cung). Xem hình dưới.

Cù lao là các điểm A và B, bờ sông là các điểm C và D. Các cây cầu trở thành các đoạn thẳng hay cung nối với các điểm trên. Ảnh minh họa.

Như vậy, Euler đã có một mô hình đơn giản nhất của bài toán 7 cây cầu, cách biểu diễn bằng các điểm và đoạn thẳng (hay cung) chính là bước đầu của sự ra đời lý thuyết đồ thị ngày nay.

Trong toán học hay tin học, lý thuyết đồ thị giúp chúng ta nghiên cứu và khảo sát các tính chất của đồ thị, trong đó đồ thị là tập hợp các đối tượng được gọi là đỉnh (nút) được nối với nhau qua các cạnh (cung).

Euler đã giải bài toán bằng cách sử dụng bậc của các nút (bậc chính là số cạnh nối với nó). Cụ thể hơn, ở bài toán 7 cây cầu có 3 nút có bậc bằng 3 và một nút có bậc là 5.

Tuy nhiên, Euler lại chứng minh bài toán chỉ có thể giải được khi không có nút bậc lẻ, mà đồ thị bài toán trên lại có tới 4 nút bậc lẻ hay nói cách khác bài toán vô nghiệm.

Vài viết gốc tại http://soha.vn/lam-the-nao-de-di-qua-ca-7-cay-cau-ma-khong-lap-lai-1-cai-nao-20170223091648886.htm